固有値 から 行列 を 求める

無効 な ms dos ファンクション です任意の固有値と固有ベクトルを持つ行列の求め方 [物理のかぎ . 固有値 から 行列 を 求める任意の固有値と固有ベクトルを持つ行列の求め方. 固有値 とそれに対応する 互いに線形独立な固有ベクトル を持つ 行列 の作り方を考えます．一見，難しそうですが， 結果は簡単です．. それでは，さっそく求めてみます．. 求めるn次正方行列 に . 四国 新聞 うち の 王様

敷布団 と マットレス どっち が いい行列の固有値・固有ベクトルの定義と具体的な計算方法 | 高校 . 実際に固有値，固有ベクトルを求めたいときには， step1：特性方程式 det (A − λ I) = 0 det(A-lambda I)=0 det (A − λ I) = 0 を解いて固有値を求める。. 固有値の定義と求め方をていねいに～計算の手順～ - 数学の景色. 実対称行列の固有値は，全て実数である。歪エルミート行列の固有値は，全て純虚数(0を含む)である。実交代行列の固有値は，全て純虚数(0を含む)である。ユニタリ行列の固有値は，全て複素平面における単位円上にある。. 固有値 から 行列 を 求める固有値と固有ベクトルとは何か？幾何学的意味と計算方法の . 固有値 から 行列 を 求める固有値と固有ベクトルの求め方. 3.1. 固有値 から 行列 を 求める固有方程式で固有値を求める. 3.2. 固有値から固有ベクトルを求める. 固有値 から 行列 を 求める3.3. 固有方程式で求められる理由. 4. 固有値と固有ベクトルの数. 4.1. 固有値が存在しない行列. 4.2. 固有値が1つの場合. 固有値 から 行列 を 求める4.3. 固有値の数を求める判別式. 5. 固有値 から 行列 を 求める固有値と固有ベクトルの計算/求め方と意味をイラストで解説!. 固有値 から 行列 を 求める行列の固有値と固有ベクトルの意味と計算の仕方. 固有値λ・固有ベクトルAの定義と求める目的. 固有値・固有ベクトルと一次変換 (本題:図解) 固有値問題 (λを求める手順) 第一段階：単位行列Eを右辺にかける. 第二段階：移項して固有ベクトルでくくる. 固有値 から 行列 を 求める第三段階：行列式から固有方程式を作る. 第四段階：固有方程式を解いて固有値を2つ求める. 固有ベクトルを求める. (1)λ＝2の時. (2)λ＝7の時. 固有値と固有ベクトルの解説 ～ 具体例と性質 ～ (証明付 . 固有方程式の解 = 固有値. 固有値 から 行列 を 求める$n$ 次正方行列 $A$ の 固有値 を $lambda$ とし、 固有値が $lambda$ になる 固有値ベクトル を $mathbf {x}_ {lambda}$ とする。 これより、 が成り立つ。 ここで $I$ は単位行列である。 この式は 同次連立一次方程式 であるので、 $mathbf {x} neq 0$ の解を持つための必要十分条件は、 係数行列 の行列式が $0$ になることである ( 「自明な解でない解を持つ ⇔ 行列式=0」 を参考)。 すなわち、 が成り立つことである。 この方程式を 固有方程式 という。. 【固有値編】固有値と固有ベクトルの求め方を解説（例題あり . 固有値と固有ベクトルの求め方. Step1. 固有方程式を解いて固有値を導く. 固有方程式とは、 lambda λ についての方程式. |A-lambda E|=0 ∣A−λE ∣ = 0. のことです。 左辺は、行列 (A-lambda E) (A− λE) の行列式です。 これの解 lambda λ が複数個見つかった場合、その全てが A A の固有値です。 Step2. 固有値に対する固有ベクトルを導く. 固有値 から 行列 を 求める固有方程式の解 lambda λ の1つ1つに対して、それぞれ連立方程式. (A-lambda E)boldsymbol {x}=boldsymbol {o} (A− λE)x = o. の非自明解（零ベクトル以外の解）を求めます。. 固有値 から 行列 を 求める固有値と固有ベクトル - Matrix calculator. 固有値 から 行列 を 求める固有値と固有ベクトルの計算. この計算機では、 特性多項式 を使用して 固有値と固有ベクトル を求めることができます。 行列 A: ( ) 対角行列. 小数を表示, 余分なセルを 空のままにしておいて 非正方行列を入力してください。 小数（有限および循環）を使用することができます： 1/3, 3.14, -1.3 (56), or 1.2e-4 ；または演算式： 2/3+3* (10-4), (1+x)/y^2, 2^0.5 (= 2), 2^ (1/3), 2^n, sin (phi), cos (3.142rad), a_1, or (root of x^5-x-1 near 1.2) 。. うさぎでもわかる線形代数 第15羽 固有値・固有ベクトル | 工業 . 固有値、固有ベクトルは微分方程式、工学、統計学など様々な場面で応用されており、期末試験、定期試験、数検、院試、編入学試験においても固有値、固有ベクトルを求める問題が超頻出します *1 。 動画で解説. 固有値の求め方についての、解説動画を作りました! こちらもぜひ参考にしてください! ★ うさぎでもわかる固有値の求め方. 固有値 から 行列 を 求める目次 [ hide] 1．固有値・固有ベクトルとは. 2．固有値・固有ベクトルの求め方. (1) 固有値の求め方. (2) 固有ベクトルの求め方. 例題1. 解説1. 例題2. 固有値 から 行列 を 求める解説2. 3．固有空間. 例題1の固有空間. 例題2の固有空間. 4．固有値計算のコツ. 固有値 から 行列 を 求める5．練習問題. 練習1. 練習2. 固有値 から 行列 を 求める練習3. 6．練習問題の答え. 解答1. 解答2. 解答3. 行列の固有値と固有ベクトル｜単位の密林. 固有値・固有ベクトルの定義から、行列を A 、固有値を λ 、固有ベクトルを x と置くと以下のように表現できる。 Ax = λx. すなわち、単位行列 E を用いた以下の方程式を解くことで固有ベクトルを求めることができる。 (A − λE)x = 0 ⋯ (∗) 方程式の導出はこちら. 当然、 (∗) 式には x = 0 という 自明な解 があるが、 今回知りたいのは 0 でない解 である。 すなわち、 (∗) 式の解が x = 0 のただ1つに決まらなければよいため、 |A − λE| = 0. なぜこのように言えるのか？ を満たす必要があり、この方程式を解けば固有値が求まる。 特に、 |A − λE| の部分を 固有多項式 と呼ぶ。 固有値・固有ベクトルの問題は、. 固有値・固有ベクトルの求め方｜固有方程式から2ステップで . 固有値 から 行列 を 求める固有方程式と固有値の求め方. 固有ベクトルの求め方. を説明します．. 固有値 から 行列 を 求めるなお，この記事の行列・ベクトルは特に断らない限り複素成分とします．. 固有値 から 行列 を 求める「線形代数学の基本」の一連の記事. 行列と列ベクトル. 1 線形代数は「多変数バージョンの比例」という話. 2 行列の計算の基本! 行列の積はなぜこうなる？ 3 連立1次方程式の掃き出し法と行列の基本変形. 4 行列とは何か？ 逆行列があると嬉しい理由. 5 正則の条件を簡単に! 基本変形と行列の積の話. 6 行列のランクと，行列が逆行列をもつための条件. 7 連立1次方程式が解をもつ条件と解の自由度. 固有値 から 行列 を 求める8 線形独立のイメージと線形独立であるための条件. 行列式. 固有値 から 行列 を 求める9 行列の正則性を判定できる行列式のイメージ. なぜ行列式を学ぶのか？ 固有値・固有ベクトルの求め方：固有 . 固有値・固有ベクトルの求め方：固有多項式の定義. 2020年12月8日 2022年1月26日. 固有値 から 行列 を 求めるどうも、木村（ @kimu3_slime ）です。 線形代数学では、 行列式 というものを学びます。 それは行列によって定まる数値ですが、一般的な定義は複雑な式になります。 なぜ行列式を学ぶのでしょうか？ ひとつの理由は、行列式は行列が表す線形変換の体積拡大率を表すものとして利用されるからです。 参考： なぜ行列式を学ぶ？ 面積・体積との一致、ヤコビアンへの応用. 固有値 から 行列 を 求めるもうひとつの理由は、 行列が逆行列を持つかどうか の判定です。 より具体的には、 固有値・固有ベクトルを求めるときに、行列式の考え方が自然に登場する ことを紹介します。 目次 [ 非表示] 固有値、固有ベクトルとは. PDF 固有値と固有ベクトル - 名古屋大学. 固有値 から 行列 を 求めるA. に対して、 A v. = v. という関係(固有方程式という)をみたすベクトル. v. = 0. を. 固有ベクトル. (eigenvector) 、スカラー.

の. 固有値. 固有値 から 行列 を 求める(eigenvalue) と呼ぶ。 をそ. 幾何学的には行列を掛けてもその方向を変えないベクトルであり、解析的には. A. 固有値 から 行列 を 求めるの冪の効果が. AN v. = N. v. のように数の冪の様子に帰着するベクトルである。 定理. 0.2. 固有値・固有ベクトル②（行列のn乗を理解する）｜行列〜線形 . 行列のn乗の計算の流れ. 2. 固有値 から 行列 を 求める固有値 ・ 固有ベクトル を用いた行列のn乗の計算の理解. 固有値 から 行列 を 求める3. まとめ. 1. 行列のn乗の計算の流れ. 固有値 から 行列 を 求める1節では行列の n 乗の計算の流れについて確認を行います。 議論の簡易化のために#3と同様に A = (2 1 1 2) の n 乗の計算について取り扱うこととします。 このとき、 固有値 λ とそれに対応する 固有ベクトル →x は#3より下記のようになります。 ・ λ = 3 のとき、 →x = t(1 1) （ t は任意の実数） ・ λ = 1 のとき、 →x = t( 1 − 1) （ t は任意の実数） 上記のように 固有値 とそれに対応する 固有ベクトル が計算できます。. 固有値，固有ベクトルの求め方. ベース ルート 弾き と は

道 に 迷っ て 目的 地 に たどり着け ない 夢(1) 行列 A の固有方程式 det (A− λ E)=0 を未知数 λ の方程式として解いて固有値 λ を求める．. A がn次正方行列のとき，固有値は[重解・虚数解も含めると]全部でn個ある．. 固有値 から 行列 を 求める(2) 各々の固有値を連立方程式 (A− λ E) →xw = →0w に代入して，対応する固有ベクトル →xw を求める．. 固有ベクトルの定数倍もまた固有ベクトルとなるので，固有ベクトルを答えるときは のように任意定数を付けた形で答えるとよい．. 例1 A= の固有値，固有ベクトルを求めよ．. （解答） (1) まず，固有方程式 det =0 を解いて固有値を求める．. (8− λ ) (5− λ )−4=0. λ2 −13 λ +40−4=0. λ2 −13 λ +36=0. 固有値と固有ベクトルの求め方を解説! | 線形代数を宇宙一 . 固有値と固有ベクトルの求め方を解説! 先生. 今回は固有値と固有ベクトルというものについて学んでいくよ! 学生. 固有値 から 行列 を 求めるはい! がんばります! さて、今回は固有値と固有ベクトルについて見ていきます。 大学の線形代数でも終盤に学ぶ内容ですが、実はそこまで難しい内容ではないんです。 図解的な理解の仕方も解説していくのでしっかり理解していきましょう! 目次. 1 固有値，固有ベクトルってなに？ 2 固有値を求めてみよう! 3 固有ベクトルを求めてみよう. 3.1 λ=5の場合. 3.2 λ=ー1の場合. 4 まとめ: 具体例で見てみると簡単. 【スポンサーリンク】 固有値，固有ベクトルってなに？ 以前の記事で線形写像について解説してきました。 関連記事. 線形写像とは何かわかりやすく解説してみる!. 行列における固有値問題の解法 | 物理学のエチュード. 行列の固有値を求める問題は 固有値問題 と呼ばれる。 固有値問題の解法. 固有値 から 行列 を 求める行列の固有値と固有ベクトルは以下のように求めます。 STEP. 固有値を求める. ( λ I n − A) x → = 0 と変形する。 非自明解 x → ( ≠ 0) が存在する条件は det ( λ I n − A) = 0 であるから、この方程式を解くことで固有値 λ が求まる。 STEP. 固有ベクトルを求める. それぞれの固有値に対して ( λ I n − A) x → = 0 から固有ベクトル x → を求める。 Φ A ( λ) ≡ det ( λ I n − A) と定義された λ の多項式 Φ A ( λ) は 固有多項式 と呼ばれ、 Φ A ( λ) = 0 は 固有方程式 と呼ばれます。 問題集. 固有値と固有ベクトルのみが分かっている状態から元の行列aを . 固有値 から 行列 を 求める行列 固有ベクトル 固有値についての問題です。 固有ベクトルを与えられている状態から、固有値の求め方がわかりません、、すみませんがよろしくお願いします! ! 1 2 1 A＝ ( 2 -2 -2 ) 1 -2 1 1 ここで、Aの固有ベクトルの1つはv1=1/√2 ( 0 ) 1 (1) v1に対応する固有値λ1を求めよ。 (2)残りの固有値λ2,λ3を求めよ。 . 数学.

大学数学についての質問です。. 皇 學 館 大学 落ち た

直 定規 と 定規 の 違い第12回 これだけ!固有ベクトルの考え方（線形代数）｜とある . 今回は固有ベクトルと固有値の考え方、つまりこれらの概念がどう大事なのかを解説します。前回の内容が理解できることが前提なので、前回の内容をしっかり復習しましょう。1．固有ベクトルで表現できること 線形空間におけるn次行列$${A}$$による線形変換を考えます。. 行列の固有値を求める - Wolfram|Alpha. 行列の固有値を求める. 自然言語. 数学入力. 固有値 から 行列 を 求める拡張キーボード. アップロード. ランダムな例を使う. 位牌 先祖 代々

ポリカ 折 板 価格何百万人もの学生やプロフェッショナルに信頼されているWolframの画期的なテクノロジーと知識ベースを使って答を計算します．数学，科学，栄養学，歴史 . 【線形代数】固有値・固有ベクトル #線形代数 - Qiita. 括った値2のことを「固有値」 同一となった値というのは向きが変わらないベクトルを「固有ベクトル」 図解 ベクトルに行列を掛け合わせると向きと大きさが変化する P_1の(1,0)に行列Aを掛け合わせることにより向きと大きさが変化する 定義式. 【対角行列】固有値方程式の固有値と固有ベクトルから対角 . Ax = αx A x = α x. 固有値 から 行列 を 求めるにおいて x x を 固有ベクトル 、 α α を 固有値 といいます。 固有値は |A − αE| = 0 | A − α E | = 0 より求めることができます。 対角行列とは 正方行列に対して対角成分以外は0である行列 のことです。 2次正方行列と3次正方行列を例にとると以下のような行列です。 行列の成分を i i 行 j j 列の成分を aij a i j とすると、 i ≠ jのとき i ≠ j の と き a_ {ij}=0である行列が対角行列といいます。. 第13回 これだけ!行列の対角化（線形代数）｜とある機械設計 . 固有値 から 行列 を 求める前回は固有値と固有ベクトルの考え方について解説しました。 今回は行列の対角化について解説します。これを学ぶことでいよいよ連成振動を解析的に解くことができるようになります。もうひと踏ん張り頑張りましょう。 1．対角行列はどうやってだすん？ 固有ベクトルと固有値の定義の式 . 固有値と固有ベクトル - MATLAB eig - MathWorks 日本. 固有値問題は、方程式 Av = λv の解を求めるものです。 ここで、A は n 行 n 列の行列、v は長さ n の列ベクトル、λ はスカラーです。 この方程式を満たす λ の値は固有値です。 この方程式を満たす v に相当する値が右固有ベクトルになります。 左固有ベクトル w は式 wA = λw を満たします。 例. 固有値 から 行列 を 求めるe = eig (A,B) は、正方行列 A および B の一般化固有値を含む列ベクトルを返します。 例. [V,D] = eig (A,B) は、一般化固有値からなる対角行列 D と、対応する右固有ベクトルを列にもつ非スパース行列 V (つまり A*V = B*V*D) を返します。. 【注意】平方和・相関行列から求めた固有値・固有ベクトルは . 平方和行列と相関係数行列から固有値・固有ベクトルを算出. 固有値 から 行列 を 求める

平方和行列と相関係数行列は関係性がある場合がある. 平方和が等しい場合. 固有値 から 行列 を 求める平方和が1の場合. 主成分分析は自分で解けます! Excelや固有値、因子負荷量とか暗記不要! 自力で導出できるぜ! 平方和行列と相関係数行列から固有値・固有ベクトルは一致しません! 一致しない理由や、一致する特別な条件は何かを解説していきます。 案外、本記事のテーマをしっかり解説した教科書はないんですよ! まず、主成分分析の基礎は関連記事で解説していますので、ご確認ください。 【重要】主成分分析が導出できる. 主成分分析で自力で主成分方向が導出できますか？ 「主成分分析＝固有値解」とインプットしていませんか？. 【線形代数】固有値・固有ベクトルとは?例題付きで分かり . 正方行列に対して 固有値・固有ベクトルはセット なりますが、全ての正方行列に存在するわけではありません。 固有ベクトルは、以下を満たすことが条件となっています。. 行列を理解する その① ベクトル、行列、テンソルの違い 行列 . 本日はいつもと趣旨を変えて数学についての記事です。 3Dグラフィックスでは、座標変換の処理で行列が一般的に使用されます。 今まで回転行列、平行移動行列、スケーリング行列についてみていきました。 しかしながら筆者自身が行列についての基礎を完全には理解していないので今回学習 . ヘッセ行列による極値判定の証明をしてみる #数学 - Qiita. Qiita初投稿になります．. 本記事では大学の微積分の講義で扱うヘッセ行列を用いた多変数関数の極値判定法の妥当性について， (ある程度)厳密な証明を作成してみます．あくまで自分なりの証明なのでレポート等で参考にする際は自己責任でお願いします . 行列の問題です。以下の問題がわかりません。(cos2θsin . 2024/3/14 18:19. 1 回答. 行列の問題です。. 以下の問題がわかりません。. 固有値 から 行列 を 求める嵐 の 湯 新潟 クーポン

日光 たまり 漬 本舗 つるや 中 禅 寺 店(cos2θ sin2θ、sin2θ -cos2θ) の固有値、固有ベクトルを求めよ。. 行列積 (cos2α sin2α、sin2α -cos2α) (cos2β sin2β、sin2β -cos2β) が回転行列になることを証明し、その回転角度を求めよ。. という . 理工学の基礎「線形代数」に心震える - 佐藤敏明 - 漫画 . つまり、文系の人間が理工学を学ぶとき、まず最初に理解しておくべき基本であるわけです。. 本書だけで、ベクトル、行列、線型空間、写像、線形変換、固有値などの線形代数の基本が文系の人間にもわかるように丁寧に解説します。. その特徴は以下の . Python, NumPyで行列の演算（逆行列、行列式、固有値など）. 本記事でもnp.matrixには触れず、np.ndarrayを使った行列演算について説明する。 SciPyを使うと要素のほとんどが0である疎行列を効率的に扱うことができる。 関連記事: Python, SciPyで疎行列の計算・処理（逆行列、固有値、連結、保存など）. うさぎでもわかる線形代数 応用編第7羽 行列の特異値分解. 固有値 から 行列 を 求めるこんにちは、. 固有値 から 行列 を 求める「うさぎでもわかる線形代数 第16羽」では正則な行列 ( P ) を用いて、行列 ( A ) を ( P^ {-1} AP ) と対角化（対角行列を作成）する方法についてお勉強しました。. こんにちは、ももやまです。. 今回は行列の対角化についてまとめていき . 固有値と固有ベクトル - Wikipedia. 固有値 から 行列 を 求める固有値や固有ベクトルの計算に対する数値的なアルゴリズムの最初のものは、ヤコビが対称行列の固有値固有ベクトルを求める手法として（ヤコビの提出したヤコビ法（電子計算機が発明されたときにフォンノイマンが発見したと思われたが実際はヤコビが . 固有ベクトル・固有値とは何か？図と具体例から分かるその意味と使い道｜アタリマエ!. 大学数学. 固有ベクトル・固有値とは何か？. 固有値 から 行列 を 求める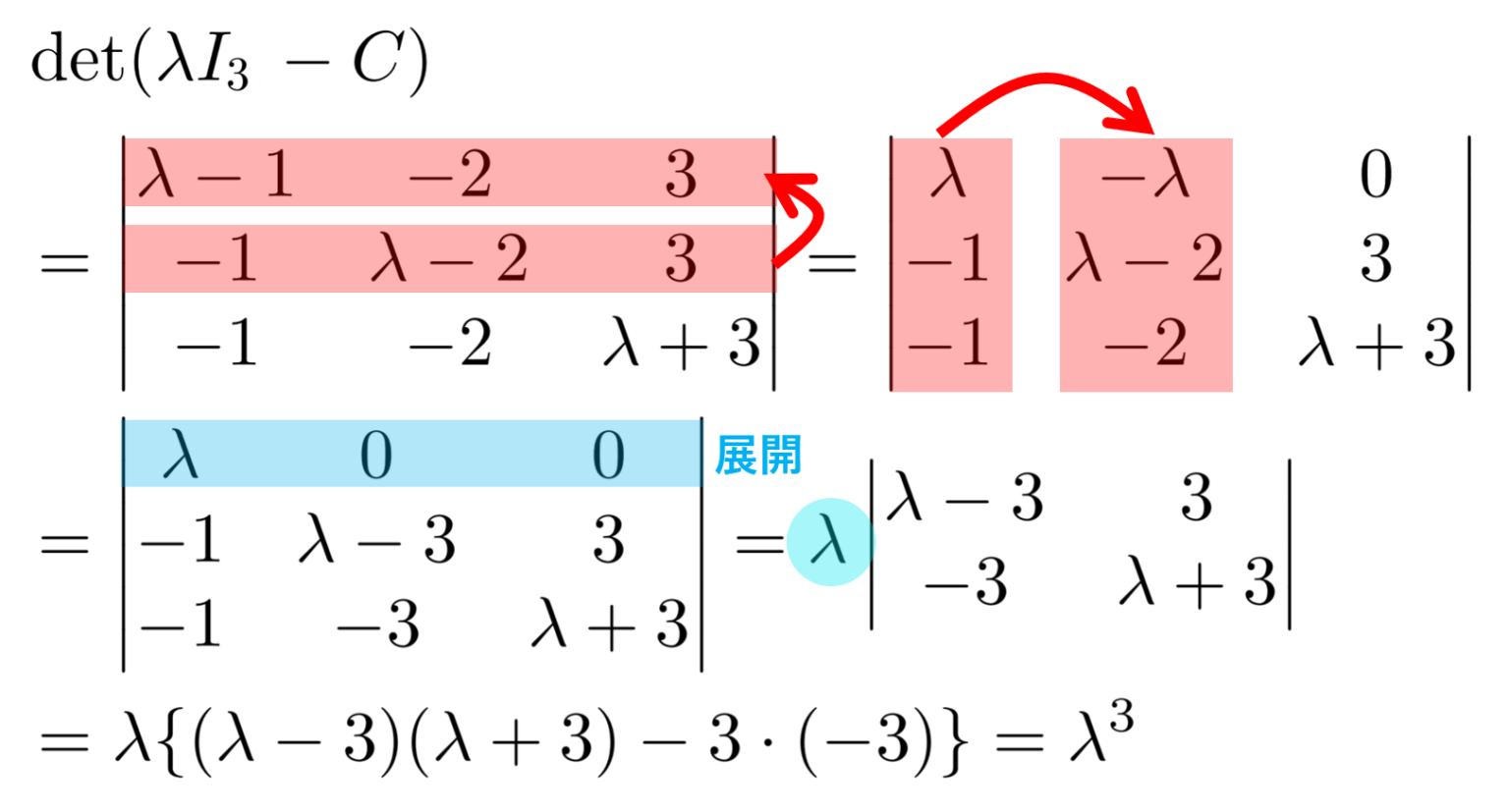

図と具体例から分かるその意味と使い道. n × n の 行列 A に対して. 固有値 から 行列 を 求めるA x → = λ x →. を満たす「 0 → でない ベクトル x → 」と「スカラー λ 」の組み合わせが存在するとき、. x → を 「A の固有ベクトル」 と言い . 線形微分方程式の解の安定性は「固有値」を調べればわかる | 趣味の大学数学. さて、線形方程式の行列(A)の固有値を調べることによって、平衡解(0)の安定性を調べることができます。 行列は、点((x,y))を別の点へ移す変換とみなせます（相図でいう矢印）。その変換はどのような性質なのかを調べるのが、固有値です。. 固有値と固有ベクトルの求め方と計算ツール - 具体例で学ぶ数学. 固有値 から 行列 を 求める算数から高度な数学まで、網羅的に解説したサイト . $2times 2$ 行列の場合には、固有値と固有ベクトルを必ず計算することができますが、$3times 3$ 行列以上になると、結果がとても汚くなる場合があります。 . 固有値を求めるときに登場した $det(A-lambda I . 固有値 から 行列 を 求める【固有値編】対角和（トレース）の意味と固有値との関係 | 大学1年生もバッチリ分かる線形代数入門. 固有方程式を、「行列の成分を用いた表現」「行列の固有値を用いた表現」の 2 通りで表すことができるということは、両者の変数の係数を比較することで、成分と固有値の間に一定の関係を見出だすことができそうです。. 固有ベクトル・固有空間の定義・求め方・性質 | 数学の景色. 固有値 から 行列 を 求めるなお， 固有ベクトルは，固有値を求めてから求めます。行列 A の固有値は，固有方程式 det(lambda I_n-A) =0 の解 lambda in mathbb{C} を求めることで求めます。 ただし， I_n は n 次単位行列を指します。固有値の個数は，重複度込みで n 個あります。. Pythonで線形代数!固有値と固有ベクトルを求める | WATLAB -Python, 信号処理, 画像処理, AI, 工学, Web-. Pythonで線形代数!固有値と固有ベクトルを求める. 行列の固有値と固有ベクトルは統計学的にも物理学的にも重要な意味を持っており、計算可能な技能を身に着けることは今では技術者として必須の項目といっても過言ではないかも知れません。. ここでは . Pythonで線形代数!行列の対角化をする方法 | WATLAB -Python, 信号処理, 画像処理, AI, 工学, Web-. 固有値 から 行列 を 求めるそして、行列Aにこの変換行列Pの逆行列を前からかけ、さらに後ろからは逆行列にしていないPをかけると、対角行列Dが求まります。 $$mathbf{D}= mathbf{P}^{-1}mathbf{A}mathbf{P}$$ しかも、対角行列の中身は対角線上に行列Aの固有値が順番に並ぶという特徴もあり . 固有値と固有ベクトル - Emanの物理数学. では次に, これらの固有ベクトルを計算で求める方法を説明しよう. 固有ベクトルを で表す. これを行列 で変換すると となる. 変換した結果, 元の を定数倍したものになるというのだから, その状況を素直に式で表すと次のようになるだろう. 行列固有値、固有ベクトル計算ツール | 科学技術計算ツール. 行列の固有値と固有ベクトルを計算するオンラインツールです。行列を入力して、[計算実行]ボタンを押すと計算結果が表示されます。実数、複素数どちらにも対応しています。固有値はQR法（原点シフト、デフレーション付き）、固有ベクトルは逆反復法で計算しています。. 固有値 から 行列 を 求める余因子と余因子行列 | 高校数学の美しい物語 - 学びTimes. 固有値 から 行列 を 求める例えば 4 × 4 4times 4 4 × 4 行列の余因子行列を計算するには， 3 × 3 3times 3 3 × 3 行列の行列式を 16 16 16 回も計算する必要があります。 実は，逆行列を計算するだけなら掃き出し法の方が簡単です。→逆行列の定義・逆行列を求める2通りの方法と例題. ユニタリ行列とは？ ～公式と性質～ (証明付) - 理数アラカルト. 正方行列 U U が を満たすとき、 が成立する。. このことから、 ユニタリ行列は U †U = I U † U = I の条件だけで定義できることが分かる。. 証明を見る. 固有値 から 行列 を 求めるユニタリ行列に関する大切な性質 (積・群・行列式・固有値・逆行列・正規直交基底)や公式・例をまとめ . 固有値を求めるプログラム - teratail【テラテイル】. 固有値 から 行列 を 求める固有値を求めるプログラム. 3次以上の行列の固有値を求めるプログラムをC言語で書こうと思っています．ただ，一般的な固有値の求め方では行列式を計算しn次方程式を解かなければなりません．3次，4次なら解の公式が一応あるらしいので，解けないことも . 【科学技術計算講座ミニ】QR法で行列の固有値を求める①. 固有値を求めるには(4)式を解けばよいのですが、行列の要素が多い場合、行列式を直接解くことは容易ではないので、別の方法が考えられています。ここではqr法という方法を紹介します。 qr法とは. qr法とは行列のqr分解を使って固有値を求める方法です。qr .

【R】固有値の計算法｜eigen関数の徹底解説｜経済統計の使い方. 固有値の計算. 固有値の計算はeigen ( )に行列名を入れれば計算できます。. 結果をeigenAとします。. 固有値 から 行列 を 求める固有値はeigenAに入っているもののうち、 $ values の3つで、大きい順に、13.7,4.9,-3.5です。. 固有ベクトルは、 $ vectors のそれぞれの列です。. 固有値 から 行列 を 求める1列目が固有値13.7に . 【科学技術計算講座ミニ】QR法で行列の固有値を求める②. a0は固有値を求める行列。nは行列の次数。eigen_valueは算出された固有値を格納する配列です。 hはa0を変換したヘッセンベルグ行列です。a0とhはprintで出力しています。 QR法. ここからがQR法のメイン部分です。. スマナビング!高校数学/物理/化学と線形代数をスマホで学ぶサイト. 線形代数を高校数学の復習も含めて、0から理解できるように解説している記事まとめです。大学生や『機械学習の原理を知る為に線形代数が必要』でも、難しい・わからない、. 主成分分析と固有値問題 | Aidemy | 10秒で始めるAIプログラミング学習サービスAidemy[アイデミー]. となる(平均値は0となっていることに注意)。これを行列の積の形に分解して表現してみると、次に示す式の一行目のようになる。実は、この分解した行列がそれぞれ. とその転置行列. になっている(実際に計算してみれば確認できる)。二行目から三行目では . 行列24の解説 （4行4列の固有値を求める） | 数学検定1級の壁. 行列24の解説 （4行4列の固有値を求める）. Tweet. 固有値 から 行列 を 求める数学検定1級合格レベルに上げる参考書. 固有値 から 行列 を 求める次の行列の固有値を求めなさい。. (11 8 5 10 14 1 4 15 2 13 16 3 7 12 9 6) |11 − λ 8 5 1 14 1 − λ 4 15 2 13 16 − λ 3 7 12 9 6 − λ|. 第1行に第2行と第3行と第4行を加える。. = |34 − λ 34 . 固有値 から 行列 を 求める逆行列の定義・逆行列を求める2通りの方法と例題 | 高校数学の美しい物語. 操作1：ある行を定数倍する. コンバット 効果 的 な 置き 方

西府 の 森 保育園操作2：二つの行を交換する. 操作3：ある行の定数倍を別の行に加える. 掃き出し法を実際にやってみます!. bs アンテナ 工事 自分 で

袷 の 着物 に 単 衣 の 長襦袢例題. A=begin {pmatrix}1&1&-1-2&0&10&2&1end {pmatrix} A = ⎝⎛ 1 −2 0 1 0 2 −1 1 1 ⎠⎞ の逆行列を求めよ。. (A:I)=begin {pmatrix}1&1 . 固有値 から 行列 を 求めるうさぎでもわかる線形代数 第18羽 対角化を用いた行列のn乗の求め方・行列の無限乗 | 工業大学生ももやまのうさぎ塾. 固有値 から 行列 を 求めるこんにちは、ももやまです。. 固有値 から 行列 を 求める今回は行列の対角化を用いて、行列のべき乗（ n 乗）を求める方法についてまとめていきたいと思います。. 対角化を行い行列の n 乗を求める方法は期末試験、編入学試験、院試、数検など様々な試験に頻出します。. 固有値 から 行列 を 求めるセロ 弾き の ゴーシュ 最後 の セリフ

スカウト され やすい 場所 大阪前回まで . 固有値の数値計算法 | kennzoの備忘録. 固有値 から 行列 を 求める係数行列 A の固有値および固有ベクトルはそれぞれ，次のような同次方程式. (1) A y = λ y. を満たすときの λ および，自明解 ( y = 0) でない解 y である．. 上記を満たす複数個の固有値と固有ベクトルを一度に表すと. (2) A M = M D. となる．. M は固有ベクトル， D . 【漸化式】例題で学ぶ：3項間漸化式の解法（行列／特性方程式） | ばたぱら.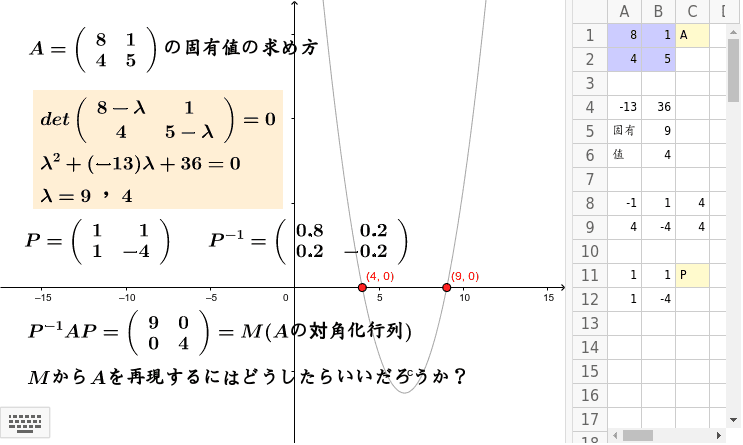

1. 紫 の 蝶 スピリチュアル

インフル エンサー に なりたい 病行列で漸化式を解く 1.1 行列で表現 例題の漸化式と等価な式を考える。以下のように考える。 そうすると、この連立方程式は行列 . を用いて、 と表すことができる。 ここで、「一般項 を求める問題」は、「 を求める問題」に置き換わった。実際、漸化 . 線形写像のランク、行列式、固有値は表現行列によらず定まることの証明 | 趣味の大学数学. 固有値 から 行列 を 求めるこれは行列(A_f,B_f)が相似であることの定義を満たします。したがって、相似な行列の一般論から、それらのランク、行列式、固有値、固有多項式、トレースが等しいことがわかりました。それらの量は、表現行列の表し方によらずに定まっています。. うさぎでもわかる線形代数 第20羽 2次形式 | 工業大学生ももやまのうさぎ塾. 直交行列を用いた対角化を行うため、行列 ( a ) の固有値、固有ベクトルを求める。 直交行列を用いた対角化について忘れてしまった人やまだわからない〜って人はこちらで復習しましょう↓ . 今日は高校生でもわかる確率から、実際に確率がどのような . 固有値 から 行列 を 求めるうさぎでもわかる線形代数 第02羽 行列と連立方程式 | 工業大学生ももやまのうさぎ塾. 今回は連立方程式を行列を使って解いてみる方法、そして連立方程式の解が係数行列、拡大係数行列の階数によってどう変わるのかなどについてまとめました。次回は、行列の割り算ともいえる逆行列の出し方についてまとめてみます。 では、また次回。. 固有空間の意味および基底や次元の求め方 - 具体例で学ぶ数学. つまり、固有空間の基底と次元を求めるためには、以下の3つの手順を行います。. 固有値 から 行列 を 求める1．. A − λE A − λ E という行列を基本変形して階段標準形 B B にする。. 2．. Bx→ = 0 B x → = 0 を満たす x x を t1x1→ + ⋯ +tdxd−→ t 1 x 1 → + ⋯ + t d x d → と表す。. 固有値 から 行列 を 求める3．固有空間 . 行列の計算—Wolfram言語ドキュメント. 行列の計算. 最新のWolfram言語には，このチュートリアルに関連する新機能が追加されている．最新情報は 行列と線形代数 を参照のこと．. このチュートリアルでは，行列の計算を実行するためのWolfram言語関数について述べる．これらの関数についての詳細 . 行列の固有多項式・最小多項式の定義・求め方・性質 | 数学の景色. n次正方行列A, Bが相似であるとは，あるn次正則行列(すなわち逆行列が存在する行列)Pが存在して，B=P^{-1}APとなることを指します。 これについて，その定義と線形写像の表現行列との関係性，性質とその証明を解説します。. 線形写像の表現行列、基底の変換の求め方を解説 | 趣味の大学数学. インプットとアウトプットを基底の線形結合で表すことで、(y=Ax)の形から(A)を求めるのが基本的な方法となります。 単に(f(x)=Ax)と覚えるのではなく（標準基底ならそれで良いのですが）、(x)、(f(x))を与えられた基底で表すときの関係式から、表現 . NumPyで行列の固有値、固有ベクトルを求めるlinalg.eig関数の使い方 - DeepAge. 固有値 から 行列 を 求めるNumPyで行列の固有値、固有ベクトルを求めるlinalg.eig関数の使い方. 固有値と固有ベクトルは行列の演算では重要な意味合いを持ってきます。. 今回はその2つを求めるための関数である linalg.eig () 関数についてみていきましょう。. ハミング符号の生成行列と検査行列の意味の理解及び誤り訂正の仕方[情報理論] - official リケダンブログ. 中華 うぶ か た

となります。wの横とGの縦の列の関係性が、下の図から見て取れると思います。 つまりハミング符号語というのは，Gとxが決まれば一意に決めることができます。逆もしかりです。 また、検査行列Hがわかるとそこから生成行列を求めることもできます。. 直交行列の5つの定義と性質の証明 | 高校数学の美しい物語. ここから，1→5→4→3を証明することで5と4を仲間に入れます。 . 固有値 から 行列 を 求める逆行列の定義・逆行列を求める2通りの方法と例題 . 線形計画法の双対定理の意味と嬉しさ . 特異値分解の定義，性質，具体例 . スカラー三重積とベクトル三重積 . 行列のn乗の求め方と例題 | 高校数学の美しい物語. 対角化できない行列の n n n 乗を計算するためには，ジョルダン標準形の知識が必要になります。→ジョルダン標準形の意味と求め方. 具体的な手順を以下に示します： J = P − 1 A P J=P^{-1}AP J = P − 1 A P となる正則行列 P P P ，ジョルダン標準形 J J J を求める . 固有空間の求め方、代数的・幾何学的重複度とは：部分空間となることの証明 | 趣味の大学数学. 固有方程式を解くには行列式の計算が、固有ベクトルを求めるには線形方程式の解き方（基本変形）といった基本的なスキルが求められます。もし途中のステップでわからない部分があれば、戻って復習してみると良いでしょう。. 分散共分散行列と相関行列の関係の導出 - からっぽのしょこ. 固有値 から 行列 を 求めるはじめに 機械学習で登場する確率分布について色々な角度から理解したいシリーズです。 この記事では、分散共分散行列と相関行列を変換する計算式を導出します。 【前の内容】 www.anarchive-beta.com 【実装編】 www.anarchive-beta.com 【他の記事一覧】 www.anarchive-beta.com 【この記事の内容】 はじめに . Julia（SymPy）で固有値、固有ベクトル、対角化、ジョルダン標準形を求める方法 | 趣味の大学数学. 以上、Julia（SymPy）で固有値、固有ベクトル、対角化、ジョルダン標準形を求める方法を紹介してきました。 今回は固有値が簡単になるような例を選びましたが、それでも対角化、ジョルダン標準形を求める計算は、手計算だと計算ミスすることもあります。. 固有値 から 行列 を 求める【C言語】行列の扱い方 | だえうホームページ. このページにはプロモーションが含まれています. このページでは、C言語での「行列の扱い方」について解説していきます。. C言語で行列を扱う方法としては様々なものが考えられますが、このページでは一番基本的な「2次元配列を行列として扱う方法」に . 広義固有空間の求め方【例題】 - Takatani Note. この記事では、広義固有空間 (一般固有空間または準固有空間)の求め方について解説します。. 固有値 から 行列 を 求める固有値や固有空間に関しては 固有値と固有多項式 または 固有空間と固有ベクトル【例題】 が詳しいです。. 固有値 から 行列 を 求めるまず, 固有空間と広義固有空間の定義を確認します . 余因子・余因子行列の求め方と例題 | AVILEN AI Trend. Facebook. ライター： nakajima_sho. 固有値 から 行列 を 求める線形代数. 当ページでは余因子と余因子行列の求め方について説明します。. 余因子行列の求め方は少し複雑で苦手とする人も多いと思いますが、ここでしっかしマスターしてしまいましょう。. 余因子 余因子 正方行列 (Aに . 固有値、固有ベクトルの幾何的な意味を考える #固有値 - Qiita. 本記事では、簡単な例を用いて 固有値 (eigenvalue) 、 固有ベクトル (eigenvector) の幾何的な意味を考えます。. 固有値、固有ベクトルと言えば、理系の大学生なら4年間付き合うことになる概念なので、式だけでなく幾何的な意味も捉えておきましょう。. 2.3.0：分散共分散行列と固有値・固有ベクトルの関係の導出【Prmlのノート】 - からっぽのしょこ. はじめに 『パターン認識と機械学習』の独学時のまとめです。一連の記事は「数式の行間埋め」または「R・Pythonでのスクラッチ実装」からアルゴリズムの理解を補助することを目的としています。本とあわせて読んでください。 また、機械学習で登場する確率分布について色々な角度から理解 . うさぎでもわかる線形代数 応用編第4羽 行列ノルム (誘導ノルム・フロベニウスノルム・最大ノルム). うさぎでもわかる線形代数 応用編第4羽 行列ノルム (誘導ノルム・フロベニウスノルム・最大ノルム) こんにちは、ももやまです。. 前回（応用編第3羽）では、ベクトルの大小を比べるための道具であるpノルム（ L p ノルム）について説明しました。. 高校 . Python (SymPy) による行列の計算 - pianofisica. 数学の具体的な計算にPythonを使って、数学もPythonも同時に学んでしまいましょう。. 今回はPythonを使って行列の計算をしてみたいと思います。. 固有値 から 行列 を 求めるPythonのごく基本的な使い方については以下の記事を参照してください：pianofisica.hatenablog.com 行列の諸操作 行列を . Pythonでの固有値分解/特異値分解のやり方を分かりやすく解説 | Brain Snacks. 固有値 から 行列 を 求める本記事ではそのような疑問に回答します。 そもそもなぜ固有値、特異値分解が機械学習を学ぶ上で必要となってくるのかその背景も踏まえて説明しますので、ぜひ参考にしてください。.